10.22235/cp.v18i1.3277

Capacidad predictiva de la flexibilidad cognitiva y la planificación en las competencias matemáticas tempranas

Predictive ability of cognitive flexibility and planning in early mathematical competencies

Capacidade preditiva da flexibilidade cognitiva e do planejamento nas competências matemáticas precoces

Francisca Bernal-Ruiz¹, ORCID 0000-0002-1240-6740

Tiare Farias², ORCID 0000-0003-2764-4431

Sofía Carreño³, ORCID 0000-0002-5781-8781

Marcela Segura⁴, ORCID 0000-0002-6485-2267

Fernanda Donoso-Alvarez⁵, ORCID 0000-0002-6485-2267

Rodrigo Rivera⁶, ORCID 0000-0002-6485-2267

¹ Universidad de Valparaíso, Chile, francisca.bernal@uv.cl

² Universidad de Valparaíso, Chile

³ Universidad de Valparaíso, Chile

⁴Universidad de Valparaíso, Chile

⁵Universidad de Valparaíso, Chile

⁶Universidad de Valparaíso, Chile

Resumen:

Se ha demostrado que las competencias matemáticas tempranas ejercen un rol importante en el aprendizaje de esta disciplina y que tanto la flexibilidad cognitiva como la planificación favorecen este proceso. Sin embargo, la mayoría de las investigaciones han relacionado las funciones ejecutivas con los resultados matemáticos generales, sin tomar en cuenta que esta disciplina incluye diversos componentes que varían en su complejidad cognitiva. Por lo tanto, el objetivo de esta investigación fue evaluar la capacidad predictiva de la flexibilidad cognitiva y la planificación en las competencias matemáticas lógico-relacionales y numéricas de 106 niños de educación inicial de escuelas chilenas, quienes fueron evaluados con dos tareas ejecutivas y un test de competencias matemáticas tempranas. Para el análisis de datos se realizaron correlaciones y modelos de regresión lineal múltiple. Los resultados mostraron que la flexibilidad cognitiva fue un predictor significativo de las competencias matemáticas tanto lógico-relacionales como numéricas, mientras que la planificación lo fue solo de las numéricas. Estos resultados confirman la importancia de la flexibilidad cognitiva y la planificación en el desarrollo de las competencias matemáticas tempranas, lo que podría propiciar intervenciones específicas sobre estas funciones ejecutivas y así favorecer el aprendizaje de las matemáticas en la educación inicial.

Palabras clave: funciones ejecutivas; flexibilidad cognitiva; competencias matemáticas tempranas; educación inicial.

Abstract:

It has been shown that early mathematical competencies play an important role in the learning of this discipline and that both cognitive flexibility and planning favor this process. However, most research has related executive functions to general mathematical outcomes, without taking into account that this discipline includes several components that vary in their cognitive complexity. Therefore, the aim of this research was to evaluate the predictive capacity of cognitive flexibility and planning in the logical-relational and numerical mathematical competencies of 106 children in early childhood education in Chilean schools, who were evaluated with two executive tasks and a test of early mathematical competencies. Correlations and multiple linear regression models were used for data analysis. The results showed that cognitive flexibility was a significant predictor of both logical-relational and numerical mathematical competencies, while planning was only a significant predictor of numerical competencies. These results confirm the importance of cognitive flexibility and planning in the development of early mathematical competencies, which could lead to specific interventions on these executive functions and thus favor the learning of mathematics in early education.

Keywords: executive functions; cognitive flexibility; early math skills; early childhood education.

Resumo:

Foi demonstrado que as competências matemáticas precoces desempenham um papel importante na aprendizagem dessa disciplina e que tanto a flexibilidade cognitiva como o planejamento favorecem esse processo. No entanto, a maioria das investigações relacionou as funções executivas com os resultados matemáticos gerais, sem ter em conta que esta disciplina inclui diversos componentes que variam na sua complexidade cognitiva. Por conseguinte, o objetivo desta investigação foi avaliar a capacidade preditiva da flexibilidade cognitiva e do planejamento nas competências matemáticas lógico-relacionais e numéricas de 106 crianças de escolas chilenas de educação infantil, que foram avaliadas com duas tarefas executivas e um teste de competências matemáticas precoces. Foram utilizados correlações e modelos de regressão linear múltipla para a análise de dados. Os resultados mostraram que a flexibilidade cognitiva foi um preditor significativo tanto das competências matemáticas lógico-relacionais como numéricas, enquanto o planejamento foi preditor significativo apenas das competências matemáticas numéricas. Estes resultados confirmam a importância da flexibilidade cognitiva e do planejamento no desenvolvimento de competências matemáticas precoces, o que poderia conduzir a intervenções específicas sobre essas funções executivas, favorecendo assim a aprendizagem da matemática na educação infantil.

Palavras-chave: funções executivas; flexibilidade cognitiva; competências matemáticas precoces; educação infantil.

Recibido: 03/03/2023

Aceptado: 22/11/2023

Es bien sabido que las competencias matemáticas tempranas (CMT) desempeñan un rol importante tanto para la educación como para el desarrollo del ser humano. Esto, debido a su utilidad para la realización de diversas actividades de la vida cotidiana y la adaptación ante los desafíos del ambiente (Fisk & Lombardi, 2021; Limas et al., 2020).

A nivel conceptual, las CMT incluyen las habilidades para usar, evaluar y comprender las matemáticas en distintos contextos en el que son necesarias (Cerda et al., 2011; Cerda et al., 2012; Raghubar & Barnes, 2017). A su vez, estas habilidades incorporan una mirada interaccionista respecto del aprendizaje de las matemáticas en la infancia, en el sentido de que asumen que tanto las habilidades lógicas como las de conteo son responsables del desarrollo del sentido numérico en los niños (Cerda et al., 2012). Desde esta perspectiva, las CMT pueden ser clasificadas en dos grandes grupos: (1) las de tipo lógico relacional, que incluyen las habilidades de comparación, clasificación, correspondencia y seriación, y (2) las de tipo numérico, que comprenden las habilidades de conteo verbal, conteo estructurado, conteo resultante y conocimiento general de los números (Cerda & Pérez, 2015; Van de Rijt et al., 1999).

Dado lo anterior y considerando que las CMT son la base fundamental para la adquisición y el desarrollo de habilidades matemáticas más avanzadas en etapas posteriores del desarrollo (Purpura et al., 2017), resulta primordial estimularlas precozmente, en específico, durante el periodo de educación inicial, ya que es una etapa propicia para fortalecer y potenciar su desarrollo (Cerda et al., 2011).

A pesar de su importancia, no es frecuente la evaluación de las CMT en la educación inicial, principalmente debido a que, en Chile, son pocos los instrumentos estandarizados para hacerlo (Cerda et al., 2012). La mayoría de las evaluaciones se realizan a estudiantes de educación básica o media (Cerda et al., 2012), etapas en donde las dificultades de aprendizaje ya son evidentes y de difícil solución (Agencia de Calidad de Educación, 2020; Chu et al., 2016).

Junto con lo anterior, diversos estudios han revelado que aproximadamente un 20 % de la población infantil presenta algún tipo de dificultad en el aprendizaje de las matemáticas (Moll et al., 2014; Wang et al., 2018). Dato que es corroborado por los resultados obtenidos en Chile en la prueba TIMSS (Trends in International Mathematics and Science Study), que es la evaluación internacional que mide el rendimiento académico en Matemáticas y Ciencias de los estudiantes de 4^to y 8^vo básico (Fishbein et al., 2021). Conforme a los resultados del 2019, los estudiantes chilenos presentan un rendimiento por debajo del promedio, donde entre un 18 % a 30 % no posee los conocimientos básicos en las áreas evaluadas (Agencia de Calidad de Educación, 2020; Arias, 2020).

A la luz de estos antecedentes, se confirma la importancia de la evaluación de las CMT en la educación inicial, no solo por su innegable contribución a los resultados positivos en el desarrollo académico posterior de los niños en la escuela (ten Braak et al., 2022), sino también porque se considera que pueden ser un medio para mejorar un conjunto amplio de habilidades, como las matemáticas, el lenguaje y las funciones ejecutivas (Mattera et al., 2017).

En este sentido, varios autores (Purpura, 2017; ten Braak et al., 2022; Viterbori et al., 2015; Yang et al., 2019) han explorado el rol de las funciones ejecutivas (FE) en el desarrollo de las CMT. Las FE se consideran fundamentales para el aprendizaje de las matemáticas (Arán Filippetti & Richaud, 2017; Escobar et al., 2018; ten Braak et al., 2022), principalmente por su contribución en el procesamiento de la información para lograr un objetivo y resolver problemas (Chan & Scalise, 2022).

Las FE son una familia de procesos de orden superior que hacen posible prestar y mantener la atención, solucionar problemas, adaptarse a situaciones novedosas, tener autocontrol y disciplina, ver las cosas desde diferentes perspectivas y ajustarse al cambio (Diamond, 2020; Tirapu-Ustárroz et al., 2018). De allí su importancia en el aprendizaje y éxito escolar (Bernal-Ruiz et al., 2020).

Existen dos perspectivas teóricas respecto a la dimensionalidad de las FE. La primera hace referencia a que son un constructo unitario (Hughes et al., 2010) y la segunda, plantea que las FE son multidimensionales, esto quiere decir que, si bien son procesos independientes, estos se encuentran interrelacionados entre sí (Tirapu-Ustárroz et al., 2018). En esta última perspectiva se distinguen al menos tres dominios ejecutivos principales: la inhibición, la memoria de trabajo y la flexibilidad cognitiva (Miyake et al., 2000; Salehinejad et al., 2021). La inhibición hace referencia a la habilidad para suprimir una respuesta prepotente en pro de una más adaptativa (Coulanges et al., 2021). La memoria de trabajo se refiere a la capacidad para mantener, manipular y transformar información mientras se lleva a cabo una tarea (Allen et al., 2021). Por su parte, la flexibilidad cognitiva hace referencia a la habilidad de considerar simultáneamente diferentes opciones y cambiar la atención de manera flexible entre ellas (Chan & Scalise, 2022; Rosas et al., 2017).

De estos tres dominios ejecutivos se derivan la planificación y la resolución de problemas (Diamond, 2020), que se relacionan con la organización del pensamiento y comportamiento, y que logran anticipar consecuencias y crean y selecciona alternativas y mapas mentales para dirigir la acción en pro de una meta u objetivo (Arroyo et al., 2014; Deng et al., 2020; Diamond, 2020; Díaz et al., 2012).

Esta investigación se centra específicamente en las FE de flexibilidad cognitiva y planificación y su contribución al logro matemático en la educación inicial.

La flexibilidad cognitiva (FC) tiene relación con la habilidad para modificar un esquema mental aprendido en función de las demandas del entorno (Chan & Scalise, 2022; Legare et al., 2018; Rosas et al., 2017; Van der Ven et al., 2011). En este sentido, para Diamond (2020), la FC tiene dos subcomponentes, uno de ellos consiste en poder ver algo desde variadas perspectivas, y el otro, en la capacidad de adaptarse rápida y flexiblemente a los cambios para encontrar diversos caminos para llegar a un objetivo deseado. Dicho de otro modo, esta FE permite cambiar el foco atencional entre distintas estrategias de solución, no solo considerando variables divergentes para la resolución de problemas sino, además, anulando comportamientos automáticos (Cantin et al., 2016; Chan & Scalise, 2022; Nunes de Santana et al., 2022).

Desde el punto de vista anatómico, se sabe que la FC emerge de la corteza prefrontal (CPF) y está conectada con los ganglios basales (Cameron et al., 2010; Chakravarthy et al., 2010; Pauli et al., 2016; Stocco et al., 2010; Zink et al., 2021). En efecto, Zink et al. (2021) reconocen que la FC está conectada con áreas cerebrales específicas que están circunscritas anatómicamente a la CPF y que se pueden relacionar con un conjunto de estructuras cerebrales similares o superpuestas. En este sentido, la FC activaría grandes porciones del cerebro, lo que convergería tanto en la CPF, la corteza cingulada anterior y la corteza parietal posterior (Chakravarthy et al., 2010; Niendam et al., 2012; Stocco et al., 2010; Zink et al., 2021).

A partir de estos antecedentes, diversos autores consideran que la FC favorece la resolución de problemas matemáticos, e incluso, se erige como un predictor de los logros y desempeño matemático durante la etapa de educación inicial y escolar (Cantin et al., 2016; Magalhães et al., 2020; Nunes de Santana et al., 2022; Palacios & Bohlmann, 2020). Logros que son posibles gracias a la habilidad de cambiar de perspectiva, de adaptarse a un ambiente cambiante y de tener un pensamiento divergente (Ropovik, 2014; Titz & Karbach, 2014).

En esta misma línea, para Cheung y Chan (2022), la FC desempeñaría un papel crucial tanto para la realización del cálculo mental, como también para la resolución de problemas matemáticos complejos. Esto, debido a que la naturaleza de estas operaciones requiere una transición constante entre diferentes procesos cognitivos que permiten que se lleven a cabo procesos como la representación mental del problema, la integración de información relevante, la ideación de un plan de resolución y la ejecución de este plan, los cuales son esenciales para resolver los problemas matemáticos (Cheung & Chan, 2022; Mayer & Hegarty, 1996).

Por otra parte, la FE de planificación (PLA) permite no solo la formulación de planes de acción, sino también su ejecución y la evaluación de su eficacia (Cortés et al., 2019). Esta habilidad ejecutiva ha sido relacionada con el funcionamiento del lóbulo frontal, específicamente con la corteza prefrontal lateral, y con los núcleos caudados dorsales, los cuales desempeñan un papel fundamental en la selección de las habilidades cognitivas pertinentes para la formación de metas y objetivos y en la elaboración de los planes necesarios para alcanzarlos (Cai et al., 2016; Levy & Dubois, 2006; Luria, 1966; Turnbull, 2002). De allí su vínculo con el desempeño matemático (Agudelo et al., 2016).

En efecto, si bien la relación entre la PLA y las competencias matemáticas ha sido abordada, no ha sido tan estudiada como las otras FE, por lo que su contribución no está del todo establecida aún (Arroyo et al., 2014). No obstante, los resultados de algunas investigaciones sugieren que la PLA tiene un importante papel en el desarrollo de las habilidades matemáticas. De hecho, Cai et al. (2016) evidenciaron este rol señalando que la PLA ejerce influencia en el proceso del aprendizaje de las matemáticas, y que este proceso se produce de manera independiente de otras FE como la memoria de trabajo, por lo que, para estos autores, prestar atención a este dominio ejecutivo desde la educación inicial incrementa las posibilidades de detectar a niños con dificultades matemáticas.

En definitiva, son múltiples los estudios que han abordado la relación entre las CMT y las FE; sin embargo, en su mayoría, estas investigaciones se han centrado solo en los tres dominios ejecutivos principales (i.e., memoria de trabajo, flexibilidad cognitiva e inhibición) (Van der Ven, 2011; Viterbori et al., 2015), relacionándolos con los resultados matemáticos generales, sin considerar que esta disciplina incluye diversos componentes que varían en su complejidad cognitiva y que, por ende, es fundamental conocer de manera específica las FE que subyacen a cada uno de ellos. En este sentido, Viterbori et al. (2015) señalan que es necesario un modelo comprensivo que incluya aspectos del funcionamiento ejecutivo y diferentes componentes de las habilidades matemáticas durante las etapas iniciales del aprendizaje matemático.

A partir de lo anterior, cabe preguntarse ¿son las funciones ejecutivas de PLA y FC predictoras de las competencias matemáticas tempranas en los niños de educación inicial? A partir de esto, el presente estudio pretende aportar nuevos resultados para así complementar y profundizar en el estudio de la capacidad predictiva de los dominios de FC y PLA en las CMT y así brindar información útil al campo de conocimiento sobre la temática.

Ahora bien, considerando el marco teórico que existe actualmente sobre este tema, se espera observar una capacidad predictiva de los dos dominios ejecutivos (FC y PLA) que sea estadísticamente significativa sobre el desarrollo de las CMT. Es decir, se espera que la capacidad predictiva tanto de la FC como de la PLA sean estadísticamente significativas en el desarrollo de las competencias matemáticas lógico-relacionales y también en las de tipo numéricas de los niños de educación inicial.

El objetivo principal de nuestro estudio fue determinar la capacidad predictiva de la FC y la PLA en las competencias matemáticas tempranas de tipo lógico-relacionales (CMLR; comparación, clasificación, correspondencia, seriación) y de tipo numéricas (CMN; conteo verbal, conteo estructurado, conteo resultante y conocimiento general de los números) en niños de educación inicial.

Método

Diseño de investigación

Se implementó un diseño no experimental ex post facto el cual tiene por objeto examinar los efectos de un acontecimiento natural sobre un resultado posterior para establecer una asociación causal o correlacional entre ellos (Kerlinger & Lee, 2000; Portell & Vives, 2019). En este caso, se estableció la capacidad predictiva de la FC y la PLA en el desarrollo de las dimensiones de las CMT de los niños de educación inicial.

Participantes

El tipo de muestreo fue no probabilístico, por conveniencia y estuvo compuesto por 106 estudiantes de educación inicial (varones n = 47, 44.3 %; niñas n = 59, 55.7 %), pertenecientes a establecimientos educacionales (EE) públicos (n = 20, 18.9 %), subvencionados (n = 72, 67.9 %) y privados (n = 14, 13.2 %) de la región de Valparaíso, Chile. Cincuenta estudiantes eran de prekínder (47.2 %) (varones n = 22, M_edad = 5.01; niñas n = 28; M_edad= 4.89) y 56 eran de kínder (52.8 %) (varones n = 25, M_edad = 6.05; niñas n = 31; M_edad = 5.96).

Los criterios de inclusión fueron: a) estar cursando prekínder o kínder, b) contar con la autorización de sus familias para participar en la investigación a través de la firma de un consentimiento informado. Los criterios de exclusión fueron: a) presentar cualquier trastorno del desarrollo neurológico, b) estar en tratamiento farmacológico que pueda afectar el desempeño en las tareas ejecutivas, y c) no querer participar en el estudio o no contar con el consentimiento informado debidamente firmado por sus familias.

Instrumentos

Las competencias matemáticas de los participantes se evaluaron con el Test de Evaluación Matemática Temprana Utrecht (Cerda et al., 2012), el cual evalúa ocho áreas de competencia, cuatro para la dimensión lógico-relacional (i.e., comparación, correspondencia, clasificación y seriación) y cuatro para la dimensión numérica (i.e., conteo verbal, conteo estructurado, conteo resultante y conocimiento general de los números) de las CMT. Este test se aplica a niños de entre 4 y 7 años y tiene una duración aproximada de 20 a 30 minutos. Consta de 40 ítems agrupados en las ocho áreas de competencia que incluyen cinco ítems cada una. Por lo que tiene una puntuación máxima de 40 puntos, de los cuales 20 puntos corresponden a las CMT de tipo lógico relacional y 20 a las de tipo numérico. Su alfa de Cronbach reportado es de .91 (Cerda et al., 2012).

Para la evaluación de la FC se utilizó la prueba Dimensional Change Card Sort (DCCS; Zelazo, 2006), en la cual los participantes clasifican tarjetas bivalentes (por ej. camiones rojos y estrellas azules) a partir de un atributo (por ej. por color) y luego se les indica que cambien y clasifiquen las mismas tarjetas a partir de un nuevo atributo (por ej. por forma). Esta prueba se aplica a niños de 3 a 5 años y tiene una duración aproximada de 5 minutos. Su alfa de Cronbach es de .94 (Zelazo, 2006).

La PLA se evaluó utilizando el Test de Laberintos de Porteus (Porteus, 1965), que mide la capacidad de una persona para elaborar y llevar a cabo un plan de acción. Este instrumento puede ser administrado en niños a partir de los 3 años, se administra de manera individual y tiene una duración aproximada de 10 minutos. Cuenta con 12 laberintos de dificultad creciente, en los cuales se debe localizar y dibujar con un lápiz la ruta más corta desde el inicio hasta el final del laberinto sin entrar en una calle sin salida. Este instrumento tiene una adecuada consistencia interna con un alfa de Cronbach de .81 (Krikorian & Bartok, 1998).

Procedimiento

En primer lugar, se llevó a cabo una reunión con el equipo directivo de cada uno de los EE que aceptaron formar parte de la investigación, en donde se les explicó el objetivo del estudio y, al mismo tiempo, se les pidió entregar el consentimiento informado a las familias con el fin de que pudieran firmar la autorización para la participación de los niños.

Luego, los niños cuyas familias autorizaron su participación fueron evaluados de manera individual en una sesión de aproximadamente 45 minutos durante su jornada escolar. Las evaluaciones fueron realizadas entre los meses de septiembre y octubre del 2022.

Plan de análisis de datos

En primer lugar, se hicieron análisis descriptivos para sintetizar la información demográfica de la muestra. Posteriormente, análisis de correlación para establecer la asociación entre la FC, PLA y las CMT de los participantes. Finalmente, modelos de regresión lineal múltiple jerárquica para la evaluación de la capacidad predictiva de las FE sobre las dimensiones de las CMT de los niños. Los análisis se hicieron con el software estadístico Jamovi, versión 2.2.5 (2021).

Consideraciones éticas de la investigación con seres humanos

Todos los procedimientos fueron implementados siguiendo los lineamientos de la Declaración de Singapur sobre la Integridad en la Investigación (Comisión Nacional de Investigación Científica y Tecnológica, 2010). Es por esto por lo que se definió un protocolo de consentimiento informado que fue firmado por los apoderados de los niños de la muestra, así como un asentimiento el cuál fue presentado a los participantes. Adicionalmente, el estudio contó con la aprobación del Comité de Ética de la Universidad.

Resultados

Análisis descriptivos

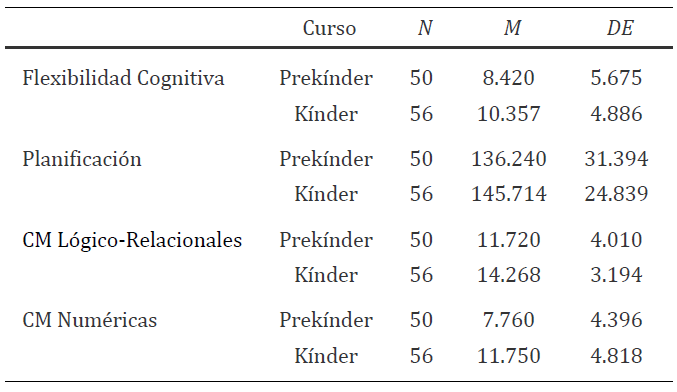
En la Tabla 1 se presentan, para cada curso, los valores promedio y desviación estándar de todas las variables de estudio.

Tabla 1: Descriptivos de las variables en estudio

Análisis de correlación entre la flexibilidad cognitiva, la planificación
y las competencias matemáticas tempranas

En primer lugar, para evaluar la capacidad predictiva de la FC y PLA sobre las CMLR y las CMN de los niños de la muestra, se analizó el supuesto de normalidad univariante para el análisis de correlación de Pearson, el cual se cumplió. Posteriormente, se generó la matriz de correlación entre las CMLR, CMN y la FC y PLA de los niños.

Se encontraron correlaciones significativas entre todas las variables (Tabla 2). En el caso de las CMLR, la correlación con la PLA es moderada (.406) y con la FC es más bien discreta (.278). Asimismo, se hallaron correlaciones significativas respecto a las CMN, con la FC (.348) y con la PLA (.263).

Tabla 2: Matriz de correlación de las competencias matemáticas con la flexibilidad cognitiva y la planificación

** p < .01 *** p < .001

Modelos de regresión lineal múltiple: FC y PLA como predictores de las competencias matemáticas de los niños

Para conocer qué FE (i.e., FC y PLA) predice las CMT (i.e., CMLR y CMN) de los participantes se empleó el análisis de regresión lineal múltiple jerárquica, donde se introdujeron como predictores las variables explicativas en función del grado de correlación con las variables dependientes de CMLR y CMN. Dado lo cual, se fueron agregando en cada uno de los modelos de regresión los dominios ejecutivos que mostraron mayor correlación con las CMT.

En la Tabla 3 se presentan los modelos testeados y se puede observar que la PLA es el mejor predictor de las CMLR, en tanto como predictor único explica el 16.5 % de la variabilidad en las CMLR. Al agregar al modelo la FC como un segundo predictor, este explica el 21.3 % y al agregar como factor el Curso, el modelo explica el 27.1 % de la variabilidad de los puntajes de los niños en las CMLR. Por lo tanto, un modelo de tres predictores compuesto por PLA, FC y curso permite predecir significativamente las CMLR, R²= 0.271, F (3, 102) = 12.6, p < .001.

Por su parte, la FC predijo de mejor manera las CMN, pues como predictor único explica el 11.9 % de la variabilidad en las CMN. Al agregar al modelo la PLA como un segundo predictor, este explica el 16.6 % y al agregar como factor el curso, el modelo explica el 26.4 % de la variabilidad de los puntajes de los niños en las CMN; sin embargo, en este último caso, la PLA deja de ser un predictor significativo (p = .051) en dicho modelo (Tabla 4). Por lo tanto, se elige un modelo de dos predictores compuesto por la FC y curso, el que permite predecir de manera significativa las CMN, R²= 0.237, F (2, 103) = 16.0, p < .001, permitiendo explicar el 23.7 % de la variabilidad de los puntajes de los niños en las CMN.

Es importante señalar que como en ambos modelos se observaron diferencias estadísticamente significativas para el factor curso (Tabla 4) —no sucedió lo mismo con sexo ni tipo de EE—, las ecuaciones de regresión introducen la variable curso dicotomizada (i.e., variable ficticia), la cual toma el valor 0 si el participante cursa prekínder y valor 1 si cursa kínder.

De esta manera, la ecuación de regresión para la variable CMLR sería: (y= α + (β₁*PLA) + (β₂*FC) + (β₃* curso dicotomizado) + ε), cuyos valores son: (y_i= 4.441 + (0.045*puntaje PLA_i) + (0.131*puntaje FC_i) + (1.865*curso_i) + ε). El subíndice i indica la persona de interés. Por otro lado, la ecuación de regresión para las CMN sería: (y= α + (β₁*FC) + (β₂* curso) + ε) y cuyos valores son: (y_i = 1.564 + (0.246*puntaje FC_i) + (3.226* curso_i) + ε). En ambas ecuaciones, γ corresponde al valor del criterio, αal valor estimado para el intercepto, β_1,β_{2 y}β₃a la estimación de los coeficientes de regresión no estandarizados de las variables (i.e., PLA, FC y Curso) y ε al error estándar de la predicción.

Tabla 3: Resumen de los modelos de regresión lineal múltiple jerárquica testeados para predecir

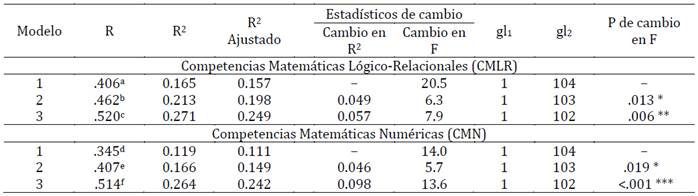
Notas: ^a Predictor: Planificación. ^b Predictores: Planificación y Flexibilidad Cognitiva. ^c Predictores: Planificación, Flexibilidad Cognitiva y Curso. ^d Predictores: Flexibilidad Cognitiva. ^ePredictores: Flexibilidad Cognitiva y Planificación.
*p < .05 ***p < .001

Tabla 4: Modelos de regresión de la flexibilidad cognitiva y planificación que predicen las competencias matemáticas de los niños y las niñas

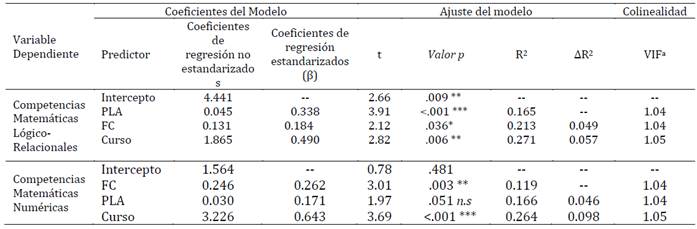
Notas: PLA: Planificación; FC: Flexibilidad Cognitiva. a. Factor de inflación de la Varianza. n.s: no significativo.

*p <.05 **p < .01 ***p < .001

Discusión

El objetivo de este estudio fue evaluar la capacidad predictiva de las funciones ejecutivas de FC y PLA en las competencias matemáticas tempranas en niños de educación inicial. Los hallazgos dan cuenta que ambas funciones tienen una capacidad predictiva en las competencias matemáticas tempranas. La FC tanto en las de tipo lógico-relacional como en las numéricas y la PLA solo en las lógico-relacionales. En este sentido, se cumplió parcialmente lo esperado, ya que la hipótesis era que la capacidad predictiva de ambas funciones ejecutivas sería significativa con respecto al desarrollo de los dos tipos de competencias matemáticas en los niños de la muestra.

A pesar de lo anterior, los hallazgos están en línea con los resultados de investigaciones que plantean que la FC está relacionada con el desempeño matemático en niños de educación inicial (Yang et al., 2019) y otros estudios como el de Cheung y Chan (2022) y el de Palacios y Bolhmann (2020), quienes concluyeron que la FC es un predictor para el desarrollo de las competencias matemáticas también en etapas posteriores de escolarización. Lo que evidencia que la FC es fundamental no solo para el cambio de foco en la representación mental de un problema y la incorporación de datos relevantes acerca del mismo, sino que también para la creación de un plan de solución y la ejecución de este, todas, habilidades que son fundamentales para resolver los problemas matemáticos (Cheung & Chan, 2022; Mayer & Hegarty, 1996). Así también, Nunes de Santana et al. (2022) concluyen que la influencia de la FC se da en ambas competencias matemáticas, tanto en las ligadas a las habilidades piagetianas, como en las de dominio numérico, lo que es confirmado por estos hallazgos.

Respecto de la influencia de la PLA en las competencias matemáticas lógico-relacionales (CMLR), este podría responder al propio proceso evolutivo de estas destrezas matemáticas, puesto que es sabido que se desarrollan a temprana edad, incluso antes del proceso de escolarización, coincidiendo con la etapa preoperatoria (Cerda et al., 2011; Piaget, 1965), de manera que los preescolares han tenido más experiencia utilizando la planificación en tareas que implican comparación, correspondencia, clasificación y seriación, que en tareas de tipo numérico (Bernal-Ruiz et al., 2022).

De igual manera, este hallazgo está en línea con otros estudios que han situado a la PLA como un buen predictor del desempeño matemático en población infantil, concluyendo que la eficiencia de los niños para resolver tareas matemáticas no se relaciona solamente con la habilidad matemática que posean, sino que depende de su habilidad para autorregularse y planificarse (Agudelo et al., 2016; Arroyo et al., 2014; Tzuriel et al., 2022), lo que corrobora que procesos como la formulación, ejecución y evaluación de un plan de acción, son necesarios para el aprendizaje de las matemáticas (Bernal-Ruiz et al., 2022).

Bajo esta misma perspectiva, y con respecto a la influencia no significativa de la PLA sobre las CMN, este hallazgo coincide con la reciente investigación de Tzuriel et al. (2022), en donde en niños de 3 a 6 años la PLA tampoco fue un predictor significativo del desempeño matemático relacionado a lo numérico. Hallazgo que se puede atribuir al desarrollo posterior que tienen las competencias numéricas respecto de las lógico-relacionales en la infancia, en tanto las primeras se desarrollan en etapas posteriores a la preoperacional (Cerda et al., 2011), y en este sentido, podrían requerir del desarrollo de las CMLR para ser adquiridas (Cerda et al., 2011; Piaget, 1965).

Bajo la misma línea, se sabe que generalmente la escolarización favorece el desarrollo de las CMN, producto de la enseñanza del sistema de numeración tradicional que se da en ese contexto (Cerda et al., 2011). Por lo tanto, al estar la muestra compuesta por niños de 4 a 6 años, es posible que presenten un desarrollo incipiente en este tipo de competencia, debido a que se encuentran en proceso de adaptación al sistema educativo. A lo anterior se suma, el desarrollo evolutivo de la PLA, la cual se forma progresivamente desde los 4 años alcanzando pleno desarrollo a los 15 años (Injoque-Ricle et al. 2014; Muchiut, 2019; Rubiales et al., 2011) debido a la maduración del lóbulo frontal durante el ciclo vital (Er-Rafiqi et al. 2022; Segundo-Marcos et al. 2022), estructura que se termina de desarrollar a finales de la infancia.

Si bien esta investigación aporta interesantes hallazgos, sobre todo respecto a la capacidad predictiva de una FE relativamente desatendida, como es la PLA en el desarrollo de las CMT, presenta algunas limitaciones. En primer lugar, el tamaño muestral fue acotado (106 niños) y el tipo de muestra intencionada, lo que restringe la posibilidad de realizar generalizaciones. Por lo que se sugiere para futuras investigaciones ampliar el tamaño muestral. En segundo lugar, no se consideró la memoria de trabajo como posible variable predictora, a pesar de haber bastante evidencia de que es una de las FE con mayor asociación con las habilidades matemáticas y la comprensión numérica (Allen et al., 2021; Bisagno et al., 2023; Peng et al., 2016). También sería interesante incluir en futuros estudios otras FE como el control inhibitorio que también es considerado un dominio ejecutivo importante en el desempeño matemático en la infancia (Cueli et al., 2020).

A pesar de estas limitaciones, el presente estudio se constituye como una contribución para la investigación de la relación de las FE de FC, PLA y el desempeño matemático en edades tempranas. Además, se erige como un aporte novedoso para la investigación, específicamente de la PLA, la cual ha sido poco estudiada y que a la luz de estos hallazgos se constituye como una variable predictora de las competencias matemáticas tempranas, específicamente de aquellas de tipo lógico-relacional.

Finalmente, a partir de los resultados de este estudio se busca brindar información útil a los educadores que pueda servir de insumo para el desarrollo de planes curriculares orientados a fortalecer el área de las matemáticas, sobre todo estimulando el desarrollo de las CMT, en tanto diversas investigaciones, no solo han evidenciado que estas competencias matemáticas constituyen un potente y estable predictor de logro del desempeño académico tanto en matemáticas como en otras áreas disciplinares (Cerda & Pérez, 2015), sino que también permiten continuar con la adquisición de conocimientos y habilidades matemáticas más complejas en las etapas escolares posteriores (Purpura et al., 2017). Además, se espera que esta investigación pueda guiar tanto a los cuidadores como a los educadores de la escolaridad inicial en el desarrollo dentro y fuera del aula estrategias de estimulación de las de las FE de FC y PLA, puesto que se ha demostrado que los niños que comienzan la educación inicial con mejores habilidades ejecutivas tienen una ventaja en términos de rendimiento matemático que persiste en los años escolares (Arroyo et al., 2014; Cervigni & Stelzer, 2011; Clements et al., 2016; Wongupparaj & Kadosh, 2022).

Referencias:

Agencia de Calidad de la Educación. (2020). Informe de Resultados Nacionales TIMSS 2019. Ministerio de Educación, Gobierno de Chile.

Agudelo, N., Dansilio, S., & Beisso, A. (2016). Diferentes tareas de solución de problemas y funciones ejecutivas en niños de 7 a 12 años. Neuropsicología Latinoamericana, 8(2), 35-42.

Allen, K., Giofrè, D., Higgins, S., & Adams, J. (2021). Using working memory performance to predict mathematics performance 2 years on. Psychological Research, 85(5), 1986-1996. https://doi.org/10.1007/s00426-020-01382-5

Arán Filippetti, V., & Richaud, M. C. (2017). A structural equation modeling of executive functions, IQ and mathematical skills in primary students: Differential effects on number production, mental calculus and arithmetical problems. Child Neuropsychology, 23, 864-888. https://doi.org/10.1080/09297049.2016.1199665

Arias, P. (2020). Análisis resultados TIMSS 2019. Acción Educar. Agencia de Calidad de la Educación. Ministerio de Educación, Gobierno de Chile.

Arroyo, M. J., Korzeniowski, C. G., & Espósito, A. V. (2014). Habilidades de planificación y organización, relación con la resolución de problemas matemáticos en escolares argentinos. Eureka, 11(1), 52-64.

Bernal-Ruiz, F., Duarte, D., Jorquera, F., Maturana, D., Reyes, C., & Santibáñez, E. (2022) Memoria de trabajo y planificación como predictores de las competencias matemáticas tempranas. Suma Psicológica, 29(2), 129–137. https://doi.org/10.14349/sumapsi.2022.v29.n2.5

Bernal-Ruiz, F., Rodríguez-Vera, M., & Ortega, A. (2020). Estimulación de las funciones ejecutivas y su influencia en el rendimiento académico en escolares de primero básico. Interdisciplinaria. Revista de Psicología y Ciencias Afines, 37(1), 1-34. http://dx.doi.org/10.16888/interd.2020.37.1.6

Bisagno, E., Cadamuro, A., & Morra, S. (2023). Multiple influences of working memory capacity on number comprehension: The interplay with metacognition and number-specific prerequisites. Journal of Experimental Child Psychology, 226, 105568. https://doi.org/10.1016/j.jecp.2022.105568

Cai, D., Georgiou, G. K., Wen, M., & Das, J. P. (2016). The role of planning in different mathematical skills. Journal of Cognitive Psychology, 28(2), 234-241. http://dx.doi.org/10.1080/20445911.2015.1103742

Cameron, I. G. M., Watanabe, M., Pari, G., & Muñoz, D. P. (2010). Executive impairment in Parkinson’s disease: response automaticity and task switching. Neuropsychologia, 48(7), 1948-1957. https://doi.org/10.1016/j.neuropsychologia.2010.03.015

Cantin, R. H., Gnaedinger, E. K., Gallaway, K. C., Hesson-McInnis, M. S., & Hund, A. M. (2016). Executive functioning predicts reading, mathematics, and theory of mind during the elementary years. Journal of Experimental Child Psychology, 146, 66-78. https://doi.org/10.1016/j.jecp.2016.01.014

Cerda, G., & Pérez, C. (2015). Predictibilidad de las competencias matemáticas tempranas, predisposición desfavorable hacia la matemática, inteligencia lógica y factores de la convivencia escolar en el rendimiento académico en matemáticas. Pensamiento Educativo, Revista de Investigación Educacional Latinoamericana, 52(2), 189-202. https://doi.org/10.7764/PEL.52.2.2015.11

Cerda, G., Pérez, C., Moreno, C., Núñez, K., Quezada, E., Rebolledo, J., & Sáez, S. (2012). Adaptación de la versión española del Test de Evaluación Matemática Temprana de Utrecht en Chile. Estudios pedagógicos, 38(1), 235-253. https://dx.doi.org/10.4067/S0718-07052012000100014

Cerda, G., Pérez, C., Ortega-Ruiz, R., Lleujo, M., & Sanhueza, L. (2011). Fortalecimiento de competencias matemáticas tempranas en preescolares, un estudio chileno. Psychology, Society, & Education, 3(1), 23-39. https://doi.org/10.25115/psye.v3i1.550

Cervigni, M. A., & Stelzer, F. (2011). Desempeño académico y funciones ejecutivas en infancia y adolescencia. Una revisión de la literatura. Revista de Investigación en Educación, 9(1), 148-156.

Chakravarthy, V. S., Joseph, D., & Bapi, R. S. (2010). What do the basal ganglia do? A modeling perspective. Biological Cybernetics. 103, 237-253. https://doi.org/10.1007/s00422-010-0401-y

Chan, J., & Scalise, N. (2022). Numeracy skills mediate the relation between executive function and mathematics achievement in early childhood. Cognitive Development, 62, 101154. https://doi.org/10.1016/j.cogdev.2022.101154

Cheung, S. K., & Chan, W. W. L. (2022). The roles of different executive functioning skills in young children’s mental computation and applied mathematical problem-solving. British Journal of Developmental Psychology, 40, 151-169. https://doi.org/10.1111/bjdp.12396

Chu, F. W., vanMarle, K., & Geary, D. C. (2016). Predicting children’s reading and mathematics achievement from early quantitative knowledge and domain-general cognitive abilities. Frontiers in Psychology, 7, 1-14. https://doi.org/10.3389/fpsyg.2016.00775

Clements, D.H., Sarama, J., & Germeroth, C. (2016). Learning executive function and early mathematics: Directions of causal relations. Early Childhood Research Quarterly, 36, 79-90. http://doi.org/10.1016/j.ecresq.2015.12.009

Comisión Nacional de Investigación Científica y Tecnológica (2010). Declaración de Singapur sobre la integridad en la investigación.

Cortés, A., Moyano, N., & Quile, A. (2019). The relationship between executive functions and academic performance in primary education: review and meta-analysis. Frontiers in Psychology, 10, 1-18. https://doi.org/10.3389/fpsyg.2019.01582

Coulanges, L., Abreu-Mendoza, R. A., Varma, S., Uncapher, M.R., Gazzaley, A., Anguera, J., & Rosenberg-Lee, M. (2021). Linking inhibitory control to math achievement via comparison of conflicting decimal numbers. Cognition, 214, 104767. https://doi.org/10.1016/j.cognition.2021.104767

Cueli, M., Areces, D., García, T., Alves, R. A., & González-Castro, P. (2020). Attention, inhibitory control and early mathematical skills in preschool students. Psicothema, 32(2), 237-244. https://doi.org/10.7334/psicothema2019.225

Deng, M., Cai, D., Zhou, X., & Leung, A. W. (2020). Executive function and planning features of students with different types of learning difficulties in Chinese junior middle school. Learning Disability Quarterly, 45(2), 134-143. https://doi.org/10.1177/0731948720929006

Diamond, A. (2020). Executive functions. In A. Gallagher, C. Bulteau, D. Cohen, & J. L. Michaud (Eds.). Handbook of Clinical Neurology, 173, 225-240. https://doi.org/10.1016/B978-0-444-64150-2.00020-4

Díaz, A., Martín, R., Jiménez, J.E., García, E., Hernández, S., & Rodríguez, C. (2012). Torre de Hanoi: datos normativos y desarrollo evolutivo de la planificación. European Journal of Education and Psychology, 5(1), 79-91. https://doi.org/10.30552/ejep.v5i1.81

Er-Rafiqi, M., Guerra, A., Le Gall, D., & Roy, A. (2022). Age-related changes of cognitive flexibility and planning skills in school-age Moroccan children. Applied Neuropsychology Child, 11(4), 669-680. https://10.1080/21622965.2021.1934471

Escobar, J. P., Rosas-Díaz, R., Ceric, F., Aparicio, A., Arango, P., Arroyo, R., Espinoza, V., Garolera, M., Pizarro, M., Porflitt, F., Ramírez, M. P., & Urzúa, D. (2018). El rol de las funciones ejecutivas en la relación entre el nivel socioeconómico y el desarrollo de habilidades lectoras y matemáticas. Cultura y Educación, 30(2), 368-392. https://doi.org/10.1080/11356405.2018.1462903

Fishbein, B., Foy, P., & Yin, L. (2021). TIMSS 2019 User Guide for the International Database (2^a ed.). International Association for the Evaluation of Educational Achievement.

Fisk, E., & Lombardi, C.M. (2021). Are math and behavioral skills interrelated? A longitudinal analysis in early childhood. Developmental Psychology, 57(12), 2106-2118. https://doi.org/10.1037/dev0001273

Hughes, C., Ensor, R., Wilson, A., & Graham, A. (2010). Tracking executive function across the transition to school: a latent variable approach. Developmental Neuropsychology, 35(1), 20-36. https://doi.org/10.1080/87565640903325691

Injoque-Ricle, I., Barreyro, J. P., Calero, A., & Burin, D. (2014). Tower of London: Planning development in children from 6 to 13 years of age. Spanish Journal of Psychology, 17(e77), 1-7. https://doi.org/10.1017/sjp.2014.83

Kerlinger, F. N., & Lee, H. B. (2000). Foundations of Behavioral Research (4^a ed.) Holt.

Krikorian, R., & Bartok, J. A. (1998). Developmental data for the Porteus Maze Test. The Clinical Neuropsychologist, 12(3), 305-310. https://doi.org/10.1076/clin.12.3.305.1984

Legare, C. H., Dale, M. T., Kim, S. Y., & Deák, G. O. (2018). Cultural variation in cognitive flexibility reveals diversity in the development of executive functions. Scientific Reports, 8(1), 1-14. https://doi.org/10.1038/s41598-018-34756-2

Levy, R., & Dubois, B. (2006). Apathy and the functional anatomy of the prefrontal cortex–basal ganglia circuits. Cerebral Cortex, 16(7), 916-928. https://doi.org/10.1093/cercor/bhj043

Limas, L.M., Novoa, P.F., Uribe, Y.C., Ramirez, Y.P., & Cancino, R.F. (2020). Competencias matemáticas en preescolares de cinco años según género. Eduser, 7(1), 41-48. https://doi.org/10.18050/eduser.v7i1.2424

Luria, A. R. (1966). Human brain and psychological processes. Harper and Row.

Magalhães, S., Carneiro, L., Limpo, T., & Filipe, M. (2020). Executive functions predict literacy and mathematics achievements: The unique contribution of cognitive flexibility in grades 2, 4, and 6. Child Neuropsychology, 26(7), 934-952. https://doi.org/10.1080/09297049.2020.1740188

Mattera, S. K., Morris, P. A., Jacob, R., Maier, M., & Rojas, N. (2017). Designing studies to test causal questions about early Math: The development of making Pre-K count. Advances in Child Development and Behavior, 53, 227-253. https://doi.org/10.1016/bs.acdb.2017.04.002

Mayer, R. E., & Hegarty, M. (1996). The process of understanding mathematical problems. In R. J. Sternberg & T. Ben-Zeev (Eds.), The Nature of Mathematical Thinking (pp. 29-53). Routledge. https://doi.org/10.4324/9780203053270

Miyake, A., Friedman, N.P., Emerson, M.J., Witzki, A.H., Howerter, A., & Wager, T.D. (2000). The unity and diversity of executive functions and their contributions to complex "Frontal Lobe" tasks: a latent variable analysis. Cognitive Psychology, 41(1), 49-100. https://doi.org/10.1006/cogp.1999.0734

Moll, K., Kunze, S., Neuhoff, N., Bruder, J., & Schultekörne, G. (2014). Specific learning disorder: prevalence and gender differences. PLOS One, 9(7), e103537. https://doi.org/10.1371/journal.pone.0103537

Muchiut, A. (2019). Juego y función ejecutiva de planificación en niños de nivel inicial. Cuadernos de Neuropsicología, 13(2), 163-170.

Niendam, T. A., Laird, A. R., Ray, K. L., Dean, Y. M., Glahn, D. C., & Carter, C. S. (2012). Meta-analytic evidence for a superordinate cognitive control network subserving diverse executive function. Cognitive, Affective, & Behavioral Neuroscience 12(2), 241-268. https://doi.org/10.3758/s13415-011-0083-5

Nunes de Santana, A., Roazzi, A., & Nobre, A.P.M.C. (2022). The Relationship between Cognitive Flexibility and Mathematical Performance in Children: A Meta-Analysis. Trends in Neuroscience and Education, 28, 100179. https://doi.org/10.1016/j.tine.2022.100179

Palacios, N., & Bohlmann, N. L. (2020). Self-regulation mediates the associations between demographic characteristics and Latino children's early achievement. Journal of Applied Developmental Psychology, 70, 101166. https://doi.org/10.1016/j.appdev.2020.101166

Pauli, W. M., O’Reilly, R. C., Yarkoni, T., & Wager, T. D. (2016). Regional specialization within the human striatum for diverse psychological functions. PNAS, 113, 1907-1912. https://doi.org/10.1073/pnas.1507610113

Peng, P., Namkung, J., Barnes, M., & Sun, C. (2016). A meta-analysis of mathematics and working memory: Moderating effects of working memory domain, type of mathematics skill, and sample characteristics. Journal of Educational Psychology, 108(4), 455-473. https://doi.org/10.1037/edu0000079

Piaget, J. (1965). The Child’s conception of number. W.W. Norton.

Portell, M., & Vives, J. (2019). Investigación en Psicología y Logopedia: Introducción a los diseños experimentales, cuasi-experimentales y ex post facto. Servei de Publicacions de la Universitat Autònoma de Barcelona.

Porteus, S. D. (1965). Porteus Maze Tests: Fifty years' application. Pacific Books.

Purpura, D. J., Schmitt, S. A., & Ganley, C. M. (2017). Foundations of mathematics and literacy: The role of executive functioning components. Journal of Experimental Child Psychology, 153, 15-34. https://doi.org/10.1016/j.jecp.2016.08.010

Raghubar, K. P., & Barnes, M. A. (2017). Early numeracy skills in preschool-aged children: a review of neurocognitive findings and implications for assessment and intervention. The Clinical Neuropsychologist, 31(2), 329-351. https://doi.org/10.1080/13854046.2016.1259387

Ropovik, I. (2014). Do executive functions predict the ability to learn problem-solving principles? Intelligence, 44, 64-74. https://doi.org/10.1016/j.intell.2014.03.002

Rosas, R., Espinoza, V., Garolera, M., & San-Martín, P. (2017). Executive Functions at the start of kindergarten: are they good predictors of academic performance at the end of year one? A longitudinal study. Studies in Psychology, 38(2), 451-472. https://doi.org/10.1080/02109395.2017.1311458

Rubiales, J., Bakker, L., & Delgado Mejía, I. D. (2011). Organización y planificación en niños con TDAH: Evaluación y propuesta de un programa de estimulación. Cuadernos de Neuropsicología, 5(2), 145-161.

Salehinejad, M. A., Ghanavati, E., Rashid, M. H. A., & Nitsche, M. A. (2021). Hot and cold executive functions in the brain: A prefrontal-cingular network. Brain and Neuroscience Advances, 5, 1-19. https://doi.org/10.1177/23982128211007769

Segundo-Marcos, R., Carrillo, A.M., Fernández, V. L., & González, M. T. D. (2022). Development of executive functions in late childhood and the mediating role of cooperative learning: A longitudinal study. Cognitive Development, 63, 101219. https://doi.org/10.1016/j.cogdev.2022.101219

Stocco, A., Lebiere, C., & Anderson, J.R. (2010). Conditional routing of information to the cortex: a model of the basal Ganglia’s role in cognitive coordination. Psychological Review, 117, 541-574. https://doi.org/10.1037/a0019077

ten Braak, D., Lenes, R., Purpura, D. J., Schmitt, S.A., & Størksen, I. (2022). Why do early mathematics skills predict later mathematics and reading achievement? The role of executive function. Journal of Experimental Child Psychology, 214, 105306. https://doi.org/10.1016/j.jecp.2021.105306

Tirapu-Ustárroz, J., Bausela-Herreras, E., & Cordero-Andrés, P. (2018). Model of executive functions based on factorial analyses in child and school populations: a meta-analysis. Revista de Neurología, 67(6), 215-225. https://doi.org/10.33588/rn.6706.2017450

Titz, C., & Karbach, J. (2014). Working memory and executive functions: Effects of training on academic achievement. Psychological Research, 78(6), 852-868. https://doi.org/10.1007/s00426-013-0537-1

Turnbull, O. (2002). The executive brain: frontal lobes and the civilized mind. Neuropsychoanalysis, 4(2), 206-208. https://doi.org/10.1080/15294145.2002.10773402

Tzuriel, D., Hanuka-Levy, D., & Kashy- Rosenbaum, G. (2022). Dynamic assessment of self-regulation and planning behavior. Frontiers in Education, 7, 885170. https://doi.org/10.3389/feduc.2022.885170

Van de Rijt, B., Van Luit, J., & Pennings, A. (1999). The construction of the Utrecht Early Mathematical Competence Scales. Educational and Psychological Measurement, 59(2), 289-309. https://doi.org/10.1177/0013164499592006

Van der Ven, S. H. G., Kroesbergen, E. H., Boom, J., & Leseman, P. P. M. (2011). The development of executive functions and early mathematics: A dynamic relationship. British Journal of Educational Psychology, 82, 100-119. https://doi.org/10.1111/j.2044-8279.2011.02035.x

Viterbori, P., Usai, M.C., Traverso, L., & De Franchis, V. (2015). How preschool executive functioning predicts several aspects of math achievement in Grades 1 and 3: A longitudinal study. Journal of Experimental Child Psychology, 140, 38-55. http://dx.doi.org/10.1016/j.jecp.2015.06.014

Wang, X., Georgiou, G. K., Li, Q., & Tavouktsoglou, A. (2018). Do Chinese children with math difficulties have a deficit in executive functioning? Frontiers in Psychology, 9, 906. https://doi.org/10.3389/fpsyg.2018.00906

Wongupparaj, P., & Kadosh, R. C. (2022). Relating mathematical abilities to numerical skills and executive functions in informal and formal schooling. BMC Psychology, 10(1), 27-40. https://doi.org/10.1186/s40359-022-00740-9

Yang, X., Chung. K. K. H., & McBride, C. (2019). Longitudinal contributions of executive functioning and visual-spatial skills to mathematics learning in young Chinese children. Educational Psychology, 39(5), 678-704. https://doi.org/10.1080/01443410.2018.1546831

Zelazo, P. (2006). The Dimensional Change Card Sort (DCCS): a method of assessing executive function in children. Nature Protocols, 1, 297-301. https://doi.org/10.1038/nprot.2006.46

Zink, N., Lenartowicz, A., & Markett, S. (2021). A new era for executive function research: On the transition from centralized to distributed executive functioning. Neuroscience & Biobehavioral Reviews, 124, 235-244. https://doi.org/10.1016/j.neubiorev.2021.02.011

Financiamiento: Proyecto de Investigación Fondecyt de Iniciación n.o 11200945 “Capacidad predictiva de las funciones ejecutivas en el desarrollo de competencias matemáticas tempranas en preescolares”, financiado por la Agencia Nacional de Investigación y Desarrollo del Ministerio de Ciencia, Tecnología, Conocimiento e Innovación del Gobierno de Chile.

Disponibilidad de datos: El conjunto de datos que apoya los resultados de este estudio no se encuentra disponible.

Cómo citar: Bernal-Ruiz, F., Farias, T., Carreño, S., Segura, M., Donoso-Alvarez, F., & Rivera, R. (2024). Capacidad predictiva de la flexibilidad cognitiva y la planificación en las competencias matemáticas tempranas. Ciencias Psicológicas, 18(1), e-3277. https://doi.org/10.22235/cp.v18i1.3277

Contribución de los autores (Taxonomía CRediT): 1. Conceptualización; 2. Curación de datos; 3. Análisis formal; 4. Adquisición de fondos; 5. Investigación; 6. Metodología; 7. Administración de proyecto; 8. Recursos; 9. Software; 10. Supervisión; 11. Validación; 12. Visualización; 13. Redacción: borrador original; 14. Redacción: revisión y edición.

F. B. R. ha contribuido en 1, 2, 3, 6, 7, 10, 12, 14; T. F. en 3, 5, 13; S. C. en 3, 5, 13; M. S. en 3, 5, 13; F. D. en 3, 5, 13; R. R. en 3, 5, 13.

Editora científica responsable: Dra. Cecilia Cracco.

10.22235/cp.v18i1.3277

Original Articles

Predictive ability of cognitive flexibility and planning in early mathematical competencies

Capacidad predictiva de la flexibilidad cognitiva y la planificación en las competencias matemáticas tempranas

Capacidade preditiva da flexibilidade cognitiva e do planejamento nas competências matemáticas precoces

Francisca Bernal-Ruiz¹, ORCID 0000-0002-1240-6740

Tiare Farias², ORCID 0000-0003-2764-4431

Sofía Carreño³, ORCID 0000-0002-5781-8781

Marcela Segura⁴, ORCID 0000-0002-6485-2267

Fernanda Donoso-Alvarez⁵, ORCID 0000-0002-6485-2267

Rodrigo Rivera⁶, ORCID 0000-0002-6485-2267

¹ Universidad de Valparaíso, Chile, francisca.bernal@uv.cl

² Universidad de Valparaíso, Chile

³ Universidad de Valparaíso, Chile

⁴Universidad de Valparaíso, Chile

⁵Universidad de Valparaíso, Chile

⁶Universidad de Valparaíso, Chile

Abstract:

Keywords: executive functions; cognitive flexibility; early math skills; early childhood education.

Resumen:

Palabras clave: funciones ejecutivas; flexibilidad cognitiva; competencias matemáticas tempranas; educación inicial.

Resumo:

Palavras-chave: funções executivas; flexibilidade cognitiva; competências matemáticas precoces; educação infantil.

Received: 03/03/2023

Accepted: 22/11/2023

It is well known that Early Mathematical Competencies (EMC) perform an important role for education as well as for human development. This, due to their usefulness in the performance of diverse daily life activities and in the adaptation to environmental challenges (Fisk & Lombardi, 2021; Limas et al., 2020).

Conceptually, EMCs include the abilities to use, assess and understand mathematics in different necessary contexts (Cerda et al., 2011; Cerda et al., 2012; Raghubar & Barnes, 2017). At the same time, these skills incorporate an interactionist view regarding mathematics learning during childhood, in the sense that they assume that both logical and counting skills are responsible for the development of number sense in children (Cerda et al., 2012). From this perspective, EMCs can be classified into two big groups: (1) those of logical-relational type, which include the comparison, classification, correspondence and seriation abilities, and (2) those of numeric type, that include the abilities of verbal counting, structured counting, resultant counting and general knowledge of numbers (Cerda & Pérez, 2015; Van de Rijt et al., 1999).

Due to the previously mentioned and considering that the EMCs are the fundamental basis for the acquisition and development of more advanced mathematical skills at later stages of development (Purpura et al., 2017), is it essential to stimulate them precociously, specifically during the early childhood education period, since it is a proper stage to strengthen and enhance their development (Cerda et al., 2011).

Despite their importance, the EMCs assessment is not frequent in early childhood education, mainly because, in Chile, there are few standardized tools to perform it (Cerda et al., 2012). Most assessments are conducted for elementary and secondary school students (Cerda et al., 2012), stages where learning difficulties are already evident and hard to solve (Agencia de Calidad de Educación, 2020; Chu et al., 2016).

In addition, several studies have shown that approximately 20% of the child population presents some type of mathematical learning difficulty (Moll et al., 2014; Wang et al., 2018). This fact is corroborated by the results obtained in Chile, in the TIMSS (Trends in International Mathematics and Science Study) test, which is the international assessment that measures the academic performance in Mathematics and Science of 8th and 12th grade students (Fishbein et al., 2021). According to 2019 results, Chilean students present a below-average performance, where from 18% to 30% does not have the basic knowledge of the assessed areas (Agencia de Calidad de Educación, 2020; Arias, 2020).

Against this background, the importance of EMCs assessment in early childhood education is confirmed, not only because of its significant contribution to positive outcomes in the further academic development of children in school (ten Braak et al., 2022), but also because it is considered that they can be a mean to improve a board set of skills such as mathematics, language and the executive functions (Mattera et al., 2017)

In this regard, many authors (Purpura, 2017; ten Braak et al., 2022; Viterbori et al., 2015; Yang et al., 2019) have explored the role of executive functions (EFs) in the EMCs development. The EFs are considered essential for mathematics learning (Arán Filippetti & Richaud, 2017; Escobar et al., 2018; ten Braak et al., 2022), mainly for their contribution in processing information to achieve an objective and solve problems (Chan & Scalise, 2022).

EFs are a family of higher order processes that make it possible to pay and maintain attention, solve problems, adapt to new situations, have self-control and discipline, see things from different perspectives and adjust to change (Diamond, 2020; Tirapu-Uztárroz et al., 2018). Hence its importance in learning and school success (Bernal-Ruiz et al., 2020).

There are two theoretical perspectives regarding EFs dimensionality. The first one refers to them as a unitary construct (Hughes et al., 2010) and the second one states that EFs are multidimensional, this means that, although they are independent processes, they are interrelated with each other (Tirapu-Uztárroz et al., 2018). The latter perspective distinguishes at least 3 main executive domains: inhibition, working memory and cognitive flexibility (Miyake et al., 2000; Salehinejad et al., 2021). Inhibition refers to the ability to suppress an overbearing response in favor of a more adaptive one (Coulanges et al., 2021). Working memory refers to the capability of maintaining, manipulating and transforming information while performing a task (Allen et al., 2021). Meanwhile, cognitive flexibility refers to the ability to simultaneously consider different options and to change attention in a flexible way between them (Chan & Scalise, 2022; Rosas et al., 2017).

From these 3 executive domains derive planning and problem solving (Diamond, 2020), which are related to thinking and behavior organization, succeeding in anticipating consequences and creating and selecting options and mind maps to direct action towards a goal or objective (Arroyo et al., 2014; Deng et al., 2020; Diamond, 2020; Díaz et al., 2012).

This study is specifically focused on EFs of cognitive flexibility and planning and its contribution to mathematical achievement in early childhood education.

Cognitive flexibility (CF) is related to the ability of modifying a learned mental scheme according to environmental demands (Chan & Scalise, 2022; Legare et al., 2018; Rosas et al., 2017; Van der Ven et al., 2011). In this context, for Diamond (2020), CF has two subcomponents, one of them entails the capability of seeing something from different perspectives, and the other one, the ability to adapt quickly and flexibly to changes in order to find different ways to reach a desired goal. In other words, this EF allows the change of attentional focus between diverse solving strategies, not only considering divergent variables for problem solving, but also cancelling automatic behaviors (Cantin et al., 2016; Chan & Scalise, 2022; Nunes de Santana et al., 2022).

From the anatomical point of view, CF is known to emerge from the prefrontal cortex (PFC) and is connected to the basal ganglia (Cameron et al., 2010; Chakravarthy et al., 2010; Pauli et al., 2016; Stocco et al., 2010; Zink et al., 2021). Indeed, Zink et al. (2021) recognize that CF is connected to specific brain areas anatomically confined to PFC and can be related to a set of similar or overlapping brain structures. In this sense, CF would activate big brain portions, converging in PFC the anterior cingulate cortex and the posterior parietal cortex (Chakravarthy et al., 2010; Niendam et al., 2012; Stocco et al., 2010; Zink et al., 2021).

From this background, many authors consider that CF favors mathematical problem solving, and even, stands as an achievements and mathematical performance predictor during the stage of early childhood and school education (Cantin et al., 2016; Magalhães et al., 2020; Nunes de Santana et al., 2022; Palacios & Bohlmann, 2020). Achievements that are possible due to the ability of perspective changing, adapting to a changing environment, and having a divergent thinking (Ropovik, 2014; Titz & Karbach, 2014).

In the same vein, to Cheung and Chan (2022), CF would play a crucial role for both mental calculation execution and complex mathematical problem solving. This, because the nature of these operations requires a constant transition between different cognitive processes that allow processes to be carried out, such as the problem mental representation, the relevant information integration, a resolution plan design and the execution of this plan, which are essential for mathematical problem solving (Cheung & Chan, 2022; Mayer & Hegarty, 1996).

On the other hand, as stated previously, the Planning allows not only the formulation of action plans, but also their execution and their effectiveness assessment (Cortés et al., 2019). This executive function has been associated with the frontal lobe functioning, specifically with the lateral prefrontal cortex and the dorsal caudate nuclei, which play an important role in selecting cognitive abilities appropriate for the formation of goals and objectives and in the development of necessary plans to achieve them. (Cai et al., 2016; Levy & Dubois, 2006; Luria, 1966; Turnbull, 2002). Thence its link with mathematical performance (Agudelo et al., 2016).

Indeed, although the relation between Planning and mathematical competencies has been addressed, it has not been as studied as the other EFs, consequently, its contribution has not been fully established yet (Arroyo et al., 2014). However, results from some studies suggest that Planning plays an important role in the development of mathematical skills. In fact, Cai et al. (2016) demonstrated this role by pointing out that Planning exerts influence during the mathematics learning process and that this process occurs independently of the others EFs such as working memory, consequently, for these authors, paying attention to this executive domain since early childhood education increases the chances of detecting children with mathematical difficulties.

In short, there are multiple studies that have addressed the relation between EMCs and EFs, however, most of these studies have focused only on the three main executive domains (i.e., working memory, cognitive flexibility and inhibition) (Van der Ven, 2011; Viterbori et al., 2015), relating them to general mathematical results, without taking into account that this discipline includes many components, which vary depending on their cognitive complexity and, thereby, is important to know EFs that underlie each of them specifically. In this respect, Viterbori et al. (2015) point out that a comprehensive model that includes aspects of executive functioning and different components of mathematical skills during the early stages of mathematical learning is necessary.

In the basis of the foregoing, it is worth asking; Are the EFs of Planning and CF predictors of early mathematical competencies in early childhood education children? Based on this, this study intends to provide new results to existing research, in order to complement and deepen in the study of predictive capacity of CF and Planning domains in EMCs, seeking to provide useful information to the field of knowledge on the topic.

Having said that, considering the theoretical framework that currently exists about this topic, an observation of a predictive capability of the two executive domains (CF and Planning) is expected that is statistically significant on the EMCs development. In other words, predictive capability of both CF and Planning is expected to be statistically significant in the development of logical-relational mathematical competencies and also in the numeric ones of early childhood education children.

The main objective of this study was to determine the predictive capability of CF and Planning in early mathematical competencies of logical-relational (Logical-Relational MC) type (comparison, classification, correspondence, seriation) and numeric (Numeric MC) type (verbal counting, structured counting, resultant counting, and general knowledge of numbers) in early childhood education children.

Method

Research design

An ex post facto non-experimental design was applied, which aims to examine the effects of a natural event over a subsequent result, with the objective to establish a causal or correlational association between them (Kerlinger & Lee, 2000; Portell & Vives, 2019). In this case, the predictive capability of CF and Planning was established in the development of the EMCs dimensions of early childhood education children.

Participants

The sampling type was non-probabilistic for convenience and was composed by 106 early childhood education students (males n = 47, 44.3%; females n = 59, 55.7%), from public (n = 20, 18.9%), subsidized (n = 72, 67.9%) and private (n = 14, 13.2%) educational establishments from the Valparaíso region of Chile. Fifty students were from prekindergarten (47.2%) (males n = 22, average age = 5.01; females n = 28; average age = 4.89) and 56 were from kindergarten (52.8%) (males n = 25, average age = 6.05; females n = 31; average age = 5.96).

The inclusion criteria were: a) attending prekindergarten or kindergarten, b) having their families authorization to participate in the research through the signing of an informed consent. The exclusion criteria were: a) present any neurodevelopmental disorder, b) be under pharmacological treatment that may affect the executive functions performance, and c) not wanting to participate in the study or not having the informed consent duly signed by their families.

Instruments

Mathematical competencies of participants were assessed by the Utrecht Early Mathematical Assessment Test (Cerda et al., 2012), which assesses eight competence areas of EMCs, four for logical-relational dimension (i.e., comparison, correspondence, classification, and seriation) and four for numeric dimension (i.e., verbal counting, structured counting, resultant counting and general knowledge of numbers). This test is applied to children between 4 and 7 years old and lasts from 20 to 30 minutes approximately. It consists of 40 items assembled in the 8 competence areas that include 5 items each. Consequently, it has a maximum score of 40 points, of which 20 points belong to logical-relational type EMCs and 20 to numeric type ones. Its reported Cronbach's alpha is .91 (Cerda et al., 2012).

For CF assessment, the Dimensional Change Card Sort (DCCS) test (Zelazo, 2006) was used, in which participants classify bivalent cards (e.g. red trucks and blue stars) based on an attribute (e.g. by color) and then, they are asked to change and classify the same cards based on a new attribute (e.g. by shape). This test is applied to children from 3 to 5 years old and lasts approximately 5 minutes. Its Cronbach's alpha is .94 (Zelazo, 2006).

The Planning was assessed using the Porteus Maze Test (Porteus, 1965), that measures a person's ability to develop and carry out an action plan. This instrument can be administered in children from 3 years old, it is administered individually and lasts approximately 10 minutes. It has 12 mazes of increasing difficulty, in which the child must locate and draw with a pencil the shortest route from the beginning to the end of the maze without entering a dead-end street. This instrument has an adequate internal consistency with a Cronbach's alpha of .81 (Krikorian & Bartok, 1998).

Procedure

Firstly, a meeting was held with the management team of each educational establishment that accepted to be part of the study, where they were explained the study objective and, at the same time, they were asked to hand the informed consent to the families in order that they could sign the authorization for the children's participation.

Then, children whose families authorized their participation were individually assessed in a session of approximately 45 minutes during their school day. Assessments were carried out between September and October 2022.

Data analysis plan

Firstly, descriptive analyses to synthesize sample demographic information were carried out. Subsequently, correlation analyses to establish association between participants’ CF, Planning and EMCs were made. Finally, multiple hierarchical linear regression models for the assessment of EFs predictive capability over children EMCs dimensions were made. Analyses were made with the Jamovi statistical software, 2.2.5 version (The jamovi project, 2021).

Ethical considerations of human being research

All procedures were implemented following the Singapore Statement on Research Integrity (Comisión Nacional de Investigación Científica y Tecnológica, 2010) guidelines. This is why an informed consent protocol was defined, that was signed by the sample children 's guardians, as well as an assent which was shown to participants. Additionally, the study met with the approval of the University 's Ethics Committee.

Results

Descriptive analyses

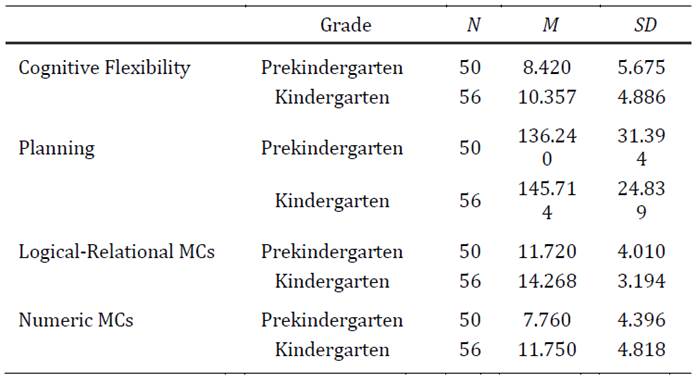
Table 1 shows, for each grade, the average values and standard deviation of all study variables.

Table 1: Descriptives of variables under study

Correlation analysis between cognitive flexibility, planning and early mathematical competencies

Firstly, to assess the predictive capability of CF and Planning over Logical-Relational MCs and Numeric MCs of the sample’s children, the univariate assumption of normality was analyzed for the Pearson correlation coefficient, which was fulfilled. Subsequently, correlation matrix was generated between the children 's Logical-Relational MCs, Numeric MCs, CF, and Planning.

Significant correlations between all variables (Table 2) were found. In the case of Logical-Relational MCs, the correlation with Planning is moderate (.406), and with CF it is rather discrete (.278). Additionally, significant correlations were found regarding Numeric MCs, with CF (.348) and Planning (.263).

Table 2: Correlation matrix of mathematical competencies with cognitive flexibility and planning

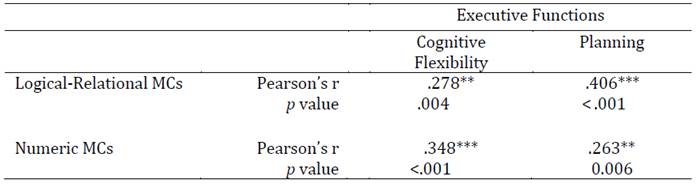
** p < .01 *** p < .001

Multiple linear regression models: CF and Planning as predictors of children's mathematical competencies

In order to know which EF (i.e., CF and Planning) predicts EMCs (i.e., Logical-Relational MC and Numeric MC) of the participants, a multiple hierarchical linear regression analysis was applied, where the explanatory variables were introduced as predictors according to the degree of correlation with the dependent variables of Logical-Relational MCs and Numeric MCs. Given this, the executive domains that showed higher correlation with the EMCs were added in each regression model.

In Table 3 the tested models are presented, and it can be observed that Planning is the best predictor of Logical-Relational MCs, since as a single predictor it explains 16.5% of Logical-Relational MCs variability. By adding the CF to the model, as a second predictor, it explains 21.3% and when the Course is added as a factor, the model explains 27.1% of the variability of children’s scores in the Logical-Relational MCs. Therefore, a three predictor model composed by Planning, CF and Course allows to significantly predict Logical-Relational MCs, R²= 0.271, F (3, 102) = 12.6, p < .001.

Meanwhile, CF predicted the Numeric MC in a better way, since as a single predictor, it explains 11.9% of Numeric MCs variability. By adding Planning as a second predictor, it explains 16.6%, and adding the Course as a factor, the model explains 26.4% of variability of children’s scores in the Numeric MCs, however, in this last case, Planning is no longer a significant predictor (p = .051) in such model (see Table 4). Hence, only a two predictors model was left, composed by CF and Course, which allows to significantly predict the Numeric MCs, R²= 0.237, F (2, 103) = 16.0, p < .001, explaining 23.7% of variability of children's scores in the Numeric MCs.

It is important to note that as in both models, statistically significant differences were observed for the course factor (Table 4) - The same didn't happen for gender nor type of educational establishment-, the regression equations introduce the dichotomized course variable (i.e., fictitious variable), which takes the value 0 if the participant attends prekindergarten and the value 1 if she or he attends kindergarten.

Thus, the regression equation for the Logical-Relational MC variable would be: (y= α + (β₁*Planning) + (β₂*CF) + (β₃* dichotomized course) + ε), of which values are: (y_i= 4.441 + (0.045* Planning_iscore) + (0.131 CF_i score) + (1.865* course_i) + ε). The subscript “i” indicates the person of interest. On the other hand, the regression equation of Numeric MCs would be: (y= α + (β₁*CF) + (β₂* course) + ε) of which values are: (y_i = 1.564 + (0.246*CF_iscore) + (3.226* course_i) + ε). In both equations, γ corresponds to the criterion value, αto the intercept estimated value, β_1,β_{2 and}β₃to the estimate of the unstandardized regression coefficients of the variables (i.e., Planning, CF, and Course) and ε to the standard error of prediction.

Table 3: Summary of the multiple hierarchical linear regression models tested to predict

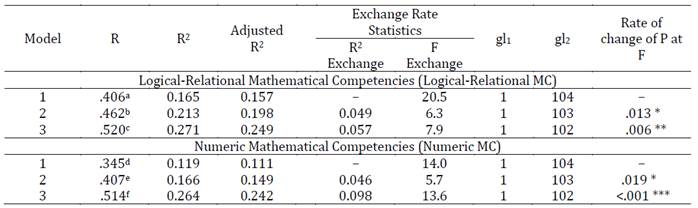
Notes. ^a Predictor: Planning. ^b Predictors: Planning and Cognitive Flexibility. ^c Predictors: Planning, Cognitive Flexibility and Course. ^d Predictors: Cognitive Flexibility. ^e Predictors: Cognitive Flexibility and Planning. ^fPredictors: Cognitive Flexibility, Planning and Course

*p < .05 ***p < .001

Table 4: Regression models of cognitive flexibility and planning predicting children's mathematical competencies

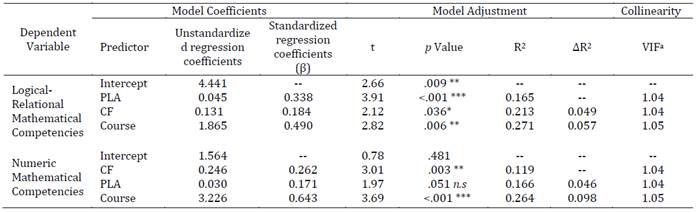
Notes: PLA: Planning; CF: Cognitive Flexibilit; n.s: not significant. a. Variance inflation factor.
*p <.05 **p < .01 ***p <.001

Discussion

The objective of this study was to assess the predictive capability of the executive functions of CF and Planning in early mathematical competencies in early childhood education children. The findings show that both functions have a predictive capability in early mathematical competencies. The CF in both logical-relational and numeric types, and Planning only in logical relational ones. In this respect, the expected was partially fulfilled, since the hypothesis was that the predictive capability from both executive functions would be significant respecting the development of both types of mathematical competencies in the sample’s children.

Despite the above, the findings are in line with the researches results that propose that the CF is related to mathematical performance in early childhood education children (Yang et al., 2019) and other studies such as the ones from Cheung and Chan (2022) and Palacios and Bolhmann (2020), who concluded that CF is a predictor for the development of mathematical competencies also in later stages of schooling. This demonstrates that CF is essential not only for the change of focus in the mental representation of a problem and the incorporation of relevant data about it, but also for the creation of a solution plan and its execution, abilities that are fundamental for solving mathematical problems (Cheung & Chan, 2022; Mayer & Hegarty, 1996). Likewise, Nunes de Santana et al. (2022) concluded that the CF influence is present in both mathematical competencies; those linked to piagetian abilities and those of numeric domain, which is confirmed by the findings of this study.

Regarding the finding of the Planning influence in logical-relational mathematical competencies (Logical-Relational MC), it is believed that this could respond to the own evolutionary process of these mathematical skills, since it is known that they develop at an early age, even before the schooling process, coinciding with the preoperative stage (Cerda et al., 2011; Piaget, 1965), in a way that preschoolers have had more experience using planning in tasks involving comparison, correspondence, classification and seriation, than in numeric type tasks (Bernal-Ruiz et al., 2022).

Similarly, this finding is in line with other studies that have placed Planning as a good predictor of mathematical performance in child population, concluding that children efficiency to solve mathematical tasks is not only related to the mathematical ability they may have, but also it depends on their ability to self-regulate and plan themselves (Agudelo et al., 2016; Arroyo et al., 2014; Tzuriel et al., 2022), which confirms that processes such as formulation, execution and assessment of an action plan are necessary for mathematics learning (Bernal-Ruiz et al., 2022).

In this same perspective, and regarding to the non-significant influence of Planning on Numeric MC, this finding coincides with the recent research of Tzuriel et al. (2022), where in children between 3 and 6 years old, Planning was not a significant predictor of numeracy-related mathematical performance either. This can be attributed to the later numeric competencies development compared to logical-relational ones in childhood, since the first ones are developed in later stages than the preoperational one (Cerda et al., 2011), and in this sense, they would require the development of Logical-Relational MCs to be acquired (Cerda et al., 2011; Piaget, 1965).

In the same vein, it is generally known that schooling favors the development of Numeric MCs, as a result of the traditional numbering system teaching that occurs in that context (Cerda et al., 2011). Therefore, as the sample is composed of children from 4 to 6 years old, it is believed that it is possible that they present an early development in this type of competence, since they are in the process of adapting to the educational system. This adds the Planning evolutionary development, which is progressively formed from 4 years old, reaching the full development at 15 years old (Injoque-Ricle et al. 2014; Muchiut, 2019; Rubiales et al., 2011) due to the frontal lobe maturation throughout the life cycle (Er-Rafiqi et al. 2022; Segundo-Marcos et al. 2022), structure that completes its development at the end of childhood.

Although this study provides interesting findings, especially regarding the predictive capability of a relatively neglected EF, such as Planning in the development of EMCs, it presents some limitations. Firstly, the sampling size was limited (106 children) and the sample type was intended, which restrains the possibility of making generalizations. Consequently, it is suggested for future studies to expand the sampling size. Secondly, working memory was not considered as a possible predictor variable, even though there is significant evidence that it is one of the EFs most associated with mathematical abilities and numeric comprehension (Allen et al., 2021; Bisagno et al., 2023; Peng et al., 2016). Additionally, it would be interesting to include in future studies other EFs, such as inhibitory control, which is also considered an important executive domain in the childhood mathematical performance (Cueli et al., 2020).

Despite these limitations, this study constitutes a contribution for research regarding the relation of EFs of CF, Planning and mathematical performance in early ages. Additionally, it stands as a novel contribution to research, specifically of Planning, which has been poorly studied and that in light of this study’s findings is constituted as a predictor variable of early mathematical competencies, specifically those of logical-relational type.

Finally, based on the results of this study, the aim is to provide teachers with useful information that may serve as an input for the development of curricular plans focused on strengthening the mathematics area, specially by stimulating the EMCs development, as well as diverse researches have not only evidenced that these mathematical competencies constitute a strong and stable predictor of achievement of the academic performance in mathematics and other disciplinary areas (Cerda & Pérez, 2015), but also allow the continuous acquisition of more complex mathematical knowledge and abilities in later schooling stages (Purpura et al., 2017). In addition, it is expected that this study can guide both caregivers and teachers of early childhood education, in order that they develop stimulation strategies of EFs, CF and Planning in-classroom and out-of-classroom, since it has been demonstrated that children that start early childhood education with better executive abilities have an advantage in terms of mathematical performance that lingers over school years (Arroyo et al., 2014; Cervigni & Stelzer, 2011; Clements et al., 2016; Wongupparaj & Kadosh, 2022).

References:

Agencia de Calidad de la Educación. (2020). Informe de Resultados Nacionales TIMSS 2019. Ministerio de Educación, Gobierno de Chile.

Agudelo, N., Dansilio, S., & Beisso, A. (2016). Diferentes tareas de solución de problemas y funciones ejecutivas en niños de 7 a 12 años. Neuropsicología Latinoamericana, 8(2), 35-42.

Arias, P. (2020). Análisis resultados TIMSS 2019. Acción Educar. Agencia de Calidad de la Educación. Ministerio de Educación, Gobierno de Chile.

Chakravarthy, V. S., Joseph, D., & Bapi, R. S. (2010). What do the basal ganglia do? A modeling perspective. Biological Cybernetics. 103, 237-253. https://doi.org/10.1007/s00422-010-0401-y

Comisión Nacional de Investigación Científica y Tecnológica (2010). Declaración de Singapur sobre la integridad en la investigación.

Fishbein, B., Foy, P., & Yin, L. (2021). TIMSS 2019 User Guide for the International Database (2^nd ed.). International Association for the Evaluation of Educational Achievement.

Kerlinger, F. N., & Lee, H. B. (2000). Foundations of Behavioral Research (4^th ed.) Holt.